今天主要是学了一些基础知识,之前一直搞面向业务开发的,老师问了一下知不知道KNN,我蒙蔽了,赶紧补补课,现在知道机器学习有三种类型:分类分析,回归分析,聚类分析。
正好我学习的KNN和集成模型都是分类分析。参考至csdn的博客。
5分类算法与应用
分类是一种常见的机器学习问题。本章首先讨论分类的基本概念、机器学习中常见的数据集,然后对KNN算法、概率模型、朴素贝叶斯分类、空间向量模型、支持向量机以及集成学习算法和应用等进行介绍。
分类问题简介
5.1.1分类算法概述
分类问题是最为常见的监督学习问题,遵循监督学习问题的基本架构和流程。一般地,分类问题的基本流程可以分为训练和预测两个阶段:
1.训练阶段。先需要准备训练数据(文本、图像、音频、视频等),然后抽取所需要的特征,形成特征数据;最后将这些特征数据连同对应的类别标记一起送入分类学习算法中,训练得到一个预测模型。
2.预测阶段。先将与训练阶段相同的特征抽取方法作用于测试数据,得到对应的特征数据;其次,使用预测模型对测试数据的特征数据进行预测;最后得到测试数据的类别标记。
监督学习可分为
分类
回归
一个关于分类学习的例子
我们来看一个问题
当我们获得一些关于肿瘤的医疗数据,我们怎么让机器判断肿瘤是良性的还是恶性的呢?

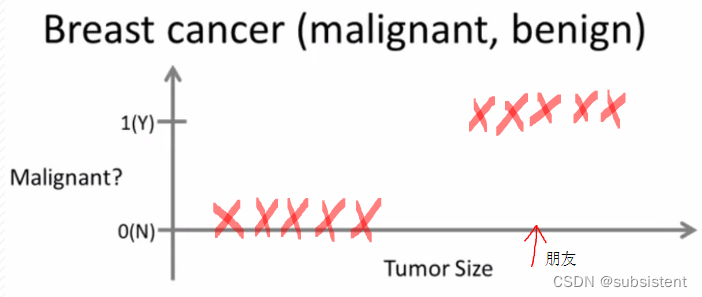
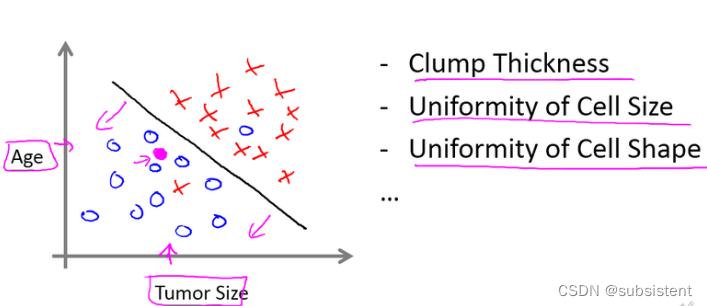
例子实现了什么?
指我们给算法一个数据集,并且给定正确答案
在分类学习中,数据集中的每个数据,算法都知道数据的“正确答案”
算法将算出更多新的结果如瘤是恶性的还是良性的
分类方法的定义
分类分析的是根据已知类别的训练集数据,建立分类模型,并利用该分类模型预测未知类别数据对象所属的类别。
分类方法的应用
模式识别(Pattern Recognition),就是通过计算机用数学技术方法来研究模式的自动处理和判读
预测,从利用历史数据记录中自动推导出对给定数据的推广描述,从而能对未来数据进行类预测
分类器
分类的实现方法是创建一个分类器(分类函数或模型),该分类器能把待分类的数据映射到给定的类别中。
创建分类的过程与机器学习的一般过程一致
分类器的构建图示
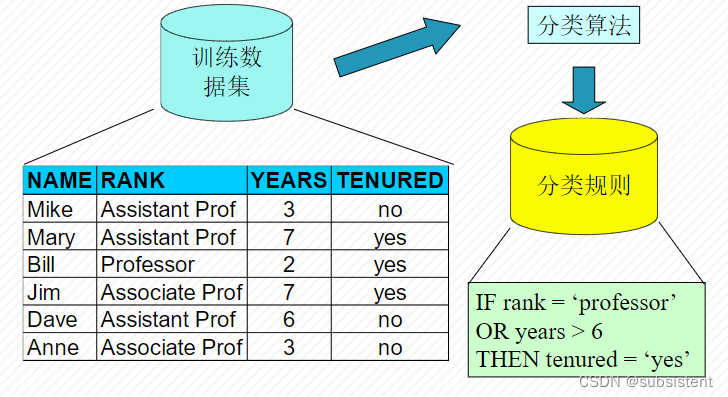
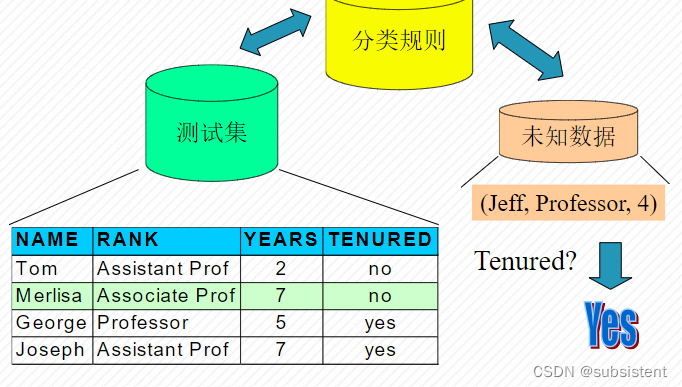
分类器的构建标准
使用下列标准比较分类和预测方法
预测的准确率:模型正确预测新数据的类编号的能力
速度:产生和使用模型的计算花销
健壮性:给定噪声数据或有空缺值的数据,模型正确预测的能力
可伸缩性:对大量数据,有效的构建模型的能力
可解释性:学习模型提供的理解和洞察的层次
鸢尾花数据集:load_iris()
iris数据集的中文名是安德森鸢尾花卉数据集,英文全称是Anderson’sIrisdataset。iris包含150个样本,对应数据集的每行数据。每行数据包含每个样本的四个特征和样本的类别信息,iris数据集是一个150行5列的二维表。
通俗地说,iris数据集是用来给花做分类的数据集,每个样本包含了花萼长度、花萼宽度、花瓣长度、花瓣宽度四个特征(前4列),我们需要建立一个分类器,分类器可以通过样本的四个特征来判断样本属于山鸢尾、变色鸢尾还是维吉尼亚鸢尾(这三个名词都是花的品种)。
iris的每个样本都包含了品种信息,即目标属性(第5列,也叫target或label)。即iris数据集每行包括4个输入变量和1个输出变量。变量名如下:
萼片长度(cm);
萼片宽度(cm);
花瓣长度(cm);
花瓣宽度(cm);
类(IrisSetosa,IrisVersicolour,IrisVirginica)。
python的机器学习库scikit已经内置了iris数据集,样本局部截图:
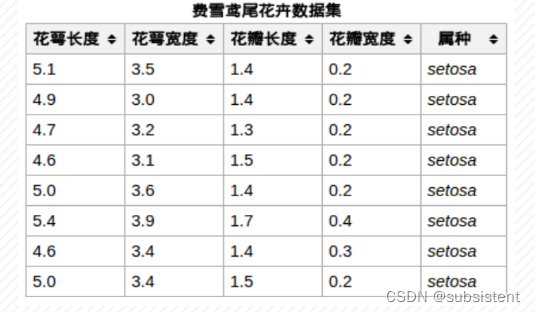
打开python集成开发环境,输入以下代码:
from sklearn import datasets
iris=datasets.load_iris()
#data对应了样本的4个特征,150行4列
print(iris.data.shape)
#显示样本特征的前5行
print(iris.data[:5])
#target对应了样本的类别(目标属性),150行1列print(iris.target.shape)
#显示所有样本的目标属性
print(iris.target)
其运行结果如下所示:
其中,iris.target用0、1和2三个整数分别代表了花的三个品种。
手写数字数据集包括1797个0-9的手写数字数据,每个数字由8*8大小的矩阵构成,矩阵中值的范围是0-16,代表颜色的深度。使用sklearn.datasets.load_digits即可加载相关数据集。其中,参数:
*return_X_y:若为True,则以(data,target)形式返回数据;默认为False,表示以字典形式返回数据全部信息(包括data和target)。
*n_class:表示返回数据的类别数,如:n_class=5,则返回0到4的数据样本。
加载数据:
from sklearn.datasets import load_digits
digits=load_digits()
print(digits.data.shape)
print(digits.target.shape)
print(digits.images.shape)
其输出结果如下所示:
(1797, 64)
(1797,)
(1797, 8, 8)
2.KNN k近邻算法
KNN算法
KNN分类器算法
K近邻(K Nearest Neighbors,KNN)算法,又称为KNN算法
思想是寻找与待分类的样本在特征空间中距离最近的K个已标记样本(即K个近邻),以这些样本的标记为参考,通过投票等方式,将占比例最高的类别标记赋给待标记样本
KNN分类器
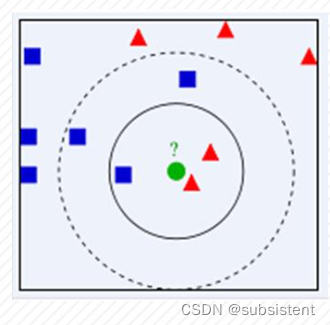
K面通过一个简单的例子说明一下:如下图,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?
集成学习
5.5.1集成模型
集成学习
定义:本身并不是一个单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务,以达到获得比单个学习器更好的学习效果的一种机器学习方法。高端点的说叫“博彩众长”,庸俗的说叫“三个臭皮匠,顶个诸葛亮”。
思路:在对新的实例进行分类的时候,把若干个单个分类器集成起来,通过对多个分类器的分类结果进行某种组合来决定最终的分类,以取得比单个分类器更好的性能。如果把单个分类器比作一个决策者的话,集成学习的方法就相当于多个决策者共同进行一项决策。
原理:生成一组个体学习器,然后采用某种策略将他们结合起来。个体学习器可以由不同的学习算法生成,之间也可以按照不同的规律生成。
集成学习的方法
目前应用较多的集成学习主要有2种:基于Boosting的和基于Bagging,前者的代表算法有Adaboost(提升树)、GBDT(梯度下降树),后者的代表算法主要是随机森林。
Boosting是个体学习器之间存在着强依赖关系,必须串行生成的序列化方法;Bagging是个体学习器之间没有强依赖关系,可同时并行生成。
Boosting之原理
从图中可以看出,首先从训练集用初始权重训练出一个弱学习器1,根据弱学习的学习误差率表现来更新训练样本的权重,使得之前弱学习器1学习误差率高的训练样本点的权重变高,使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2.,如此重复进行,直到弱学习器数达到事先指定的数目T,最终将这T个弱学习器通过集合策略进行整合,得到最终的强学习器。
个体弱学习器的训练集是通过随机采样得到的。通过T次的随机采样,我们就可以得到T个采样集,对于这T个采样集,我们可以分别独立的训练出T个弱学习器,再对这T个弱学习器通过集合策略来得到最终的强学习器。
Boosting和Bagging的区别
1、样本选择:前者每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。后者训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
2、样例权重:前者根据错误率不断调整样例的权值,错误率越大则权重越大;后者使用均匀取样,每个样例的权重相等。
3、预测函数:前者每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。后者所有预测函数的权重相等。
4、并行计算:前者各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果;后者各个预测函数可以并行生成
5.5.2决策树
树形结构都比较熟悉,由节点和边两种元素组成的结构。决策树(Decision Tree)利用树结构进行决策,每一个非叶节点是一个判断条件,每一个叶子节点是结论,从跟节点开始,经过多次判断得出结论。
决策树案例
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。
相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见。
假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员
决策树模型构造
所谓决策树的构造就是进行属性选择度量,确定各个特征属性之间的拓扑结构。关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。
决策树的分裂属性
1、属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
2、属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。
3、属性是连续值。此时确定一个值作为分裂点split_point,按照>split_point和<=split_point生成两个分支。
ID3算法
从信息论知识中我们知道,期望信息越小,信息增益越大,从而纯度越高。ID3算法的核心思想就是以信息增益度量属性选择,选择分裂后信息增益最大的属性进行分裂。
引入熵的概念:熵是表示随机变量不确定性的度量,白话称为物体内部的混乱程度。
一个例子:A集合[1,1,1,2,2] B集合[1,2,3,4,5]
显然A集合的熵值要低,因为只有两种类别,相对稳定一些;而B集合的类别太多,熵值就会大很多。
————————————————
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/m0_65121454/article/details/128178708
如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那类
如果K=5,蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类
KNN分类器算法
KNN算法需要确定K值、距离度量和分类决策规则
K值过小时,只有少量的训练样本对预测起作用,容易发生过拟合,或者受含噪声训练数据的干扰导致错误
K值过大,过多的训练样本对预测起作用,当不同类别样本数量不均衡时,结果偏向数量占优的样本
1)计算测试数据与各个训练数据之间的距离;
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。
5.2.2基于k近邻算法实现分类任务
分类、回归、聚类不同的评判指标。
分类算法中,常用的性能指标有:
1.准确率( accuracy)
2.AUC(Area Under Curve)
回归分析中,常用的性能指标有:
1.均方误差(mean_squared_error)
2.可析方差得分(explained_variance_score)
交叉验证(Cross validation):
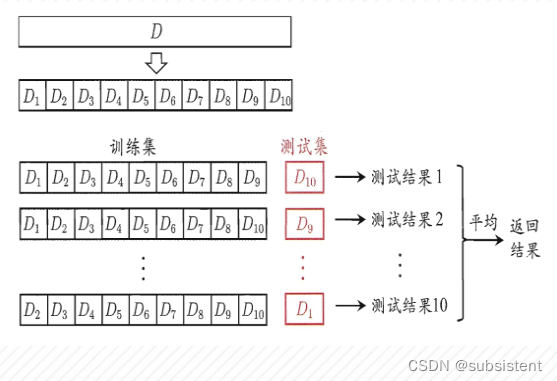
集成学习
5.5.1集成模型
集成学习
定义:本身并不是一个单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务,以达到获得比单个学习器更好的学习效果的一种机器学习方法。高端点的说叫“博彩众长”,庸俗的说叫“三个臭皮匠,顶个诸葛亮”。
思路:在对新的实例进行分类的时候,把若干个单个分类器集成起来,通过对多个分类器的分类结果进行某种组合来决定最终的分类,以取得比单个分类器更好的性能。如果把单个分类器比作一个决策者的话,集成学习的方法就相当于多个决策者共同进行一项决策。
原理:生成一组个体学习器,然后采用某种策略将他们结合起来。个体学习器可以由不同的学习算法生成,之间也可以按照不同的规律生成。
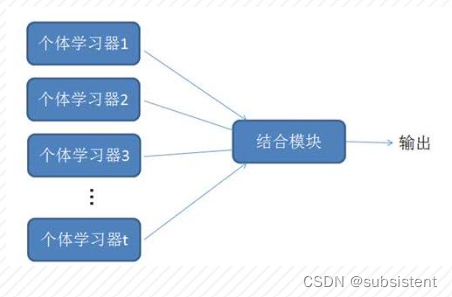
集成学习的方法
目前应用较多的集成学习主要有2种:基于Boosting的和基于Bagging,前者的代表算法有Adaboost(提升树)、GBDT(梯度下降树),后者的代表算法主要是随机森林。
Boosting是个体学习器之间存在着强依赖关系,必须串行生成的序列化方法;Bagging是个体学习器之间没有强依赖关系,可同时并行生成。
Boosting之原理
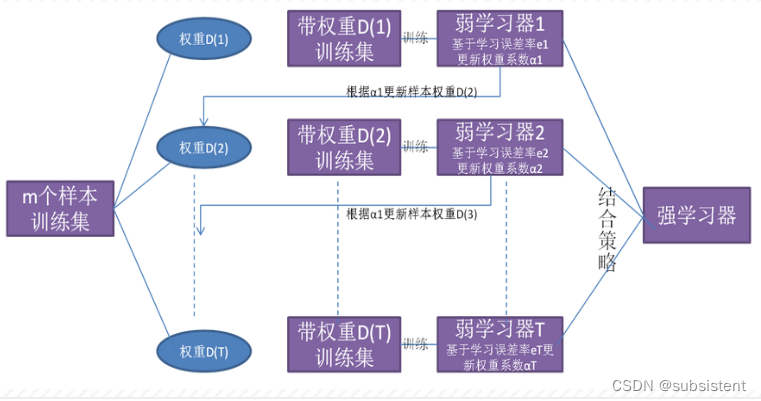
从图中可以看出,首先从训练集用初始权重训练出一个弱学习器1,根据弱学习的学习误差率表现来更新训练样本的权重,使得之前弱学习器1学习误差率高的训练样本点的权重变高,使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2.,如此重复进行,直到弱学习器数达到事先指定的数目T,最终将这T个弱学习器通过集合策略进行整合,得到最终的强学习器。

几个体弱学习器的训练集是通过随机采样得到的。通过T次的随机采样,我们就可以得到T个采样集,对于这T个采样集,我们可以分别独立的训练出T个弱学习器,再对这T个弱学习器通过集合策略来得到最终的强学习器。
Boosting和Bagging的区别
1、样本选择:前者每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。后者训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
2、样例权重:前者根据错误率不断调整样例的权值,错误率越大则权重越大;后者使用均匀取样,每个样例的权重相等。
3、预测函数:前者每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。后者所有预测函数的权重相等。
4、并行计算:前者各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果;后者各个预测函数可以并行生成
5.5.2决策树
树形结构都比较熟悉,由节点和边两种元素组成的结构。决策树(Decision Tree)利用树结构进行决策,每一个非叶节点是一个判断条件,每一个叶子节点是结论,从跟节点开始,经过多次判断得出结论。
决策树案例
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。
相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见。
假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员
决策树模型构造
所谓决策树的构造就是进行属性选择度量,确定各个特征属性之间的拓扑结构。关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。
决策树的分裂属性
1、属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
2、属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。
3、属性是连续值。此时确定一个值作为分裂点split_point,按照>split_point和<=split_point生成两个分支。
ID3算法
从信息论知识中我们知道,期望信息越小,信息增益越大,从而纯度越高。ID3算法的核心思想就是以信息增益度量属性选择,选择分裂后信息增益最大的属性进行分裂。
引入熵的概念:熵是表示随机变量不确定性的度量,白话称为物体内部的混乱程度。
一个例子:A集合[1,1,1,2,2] B集合[1,2,3,4,5]
显然A集合的熵值要低,因为只有两种类别,相对稳定一些;而B集合的类别太多,熵值就会大很多。